通过找公共因子,达到降维目的。如果变量间不相关,则不能使用因子分析降维。
最简单的因子模型
$$ x_i = F_i + \varepsilon_i
$$
$$F$$是对所以变量都起作用的因子,$$\varepsilon_i$$是第$$i$$个变量特有的,即每个变量是由一个公共因子和一个特殊因子之和组成。
因子分析的目标
- 确定是否存在更少的不想关变量,他们能解释原始变量之间的关系
- 确定因子的个数
- 解释这些因子
计算因子得分
将因子作为进一步统计分析的变量,比如对原始变量或$$n$$个实验单元进行分类
因子分析与主成分的区别
- 主成分分析不是一个模型,只是变量的变换,而因子分析需要构建模型
- 主成分是原始变量的线性组合,而在因子分析中,原始变量是公共因子和特殊因子的线性组合
- 主成分和原始变量无因果关系,而因子分析中,因子是因,原始变量是果
- 标准化对主成分分析有影响,但是对因子分析无影响
- 主成分个数与原始变量个数一样(解释所有的方差),因子个数通常比原始变量个数少(达到降维目的)
- 主成分关心的是变量的方差,因子分析更关心变量的协方差或相关矩阵(标准化后的相关系数矩阵)的结构
- 主成分分析不能旋转,而因子分析通过旋转可以使得因子有很好的解释结果
- 因子分析结果不是唯一的,而主成分分析的结果是唯一的
- 主分量分析是将原始变量的方差尽量分解在前面的主分量上,因子分析是将协方差分解在因子载荷上,方差还可以放在特殊因子的方差上
正交因子模型
公共因子$$F$$间不相关,所以是正交模型;特殊因子间不相关可以更好的解释,公共的部分都被公共因子提取出来了,所以特殊因子不相关;公共因子不相关的假设有可能是不符合实际的;要根据实际问题确定是否对原始变量进行标准化。

其中$$x$$为已知的$$p$$维原始变量,$$F$$为待提取的$$m$$维因子,$$\varepsilon$$为特殊因子。
模型中的$$\Lambda=(\lambdaij ){(p×m)}$$为待估计的系数矩阵,即因子载荷矩阵,$$\lambda_{ij}$$为第$$i$$个变量在第$$j$$个因子上的载荷。
因子分析方程
因子载荷矩阵$$\Lambda$$不唯一,模型不受量纲影响
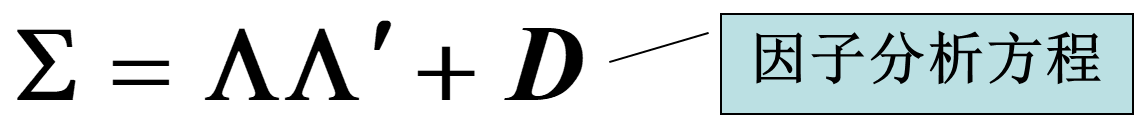
推导过程
因子载荷矩阵是原始变量和公共因子间的协方差矩阵
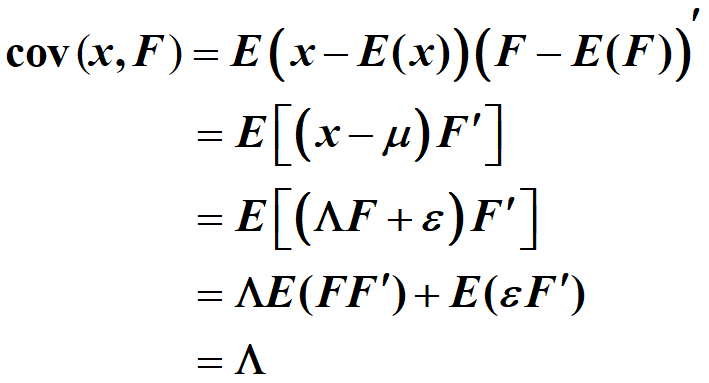
原始变量的方差$$S$$可以分解在因子载荷矩阵上和特殊因子的方差上
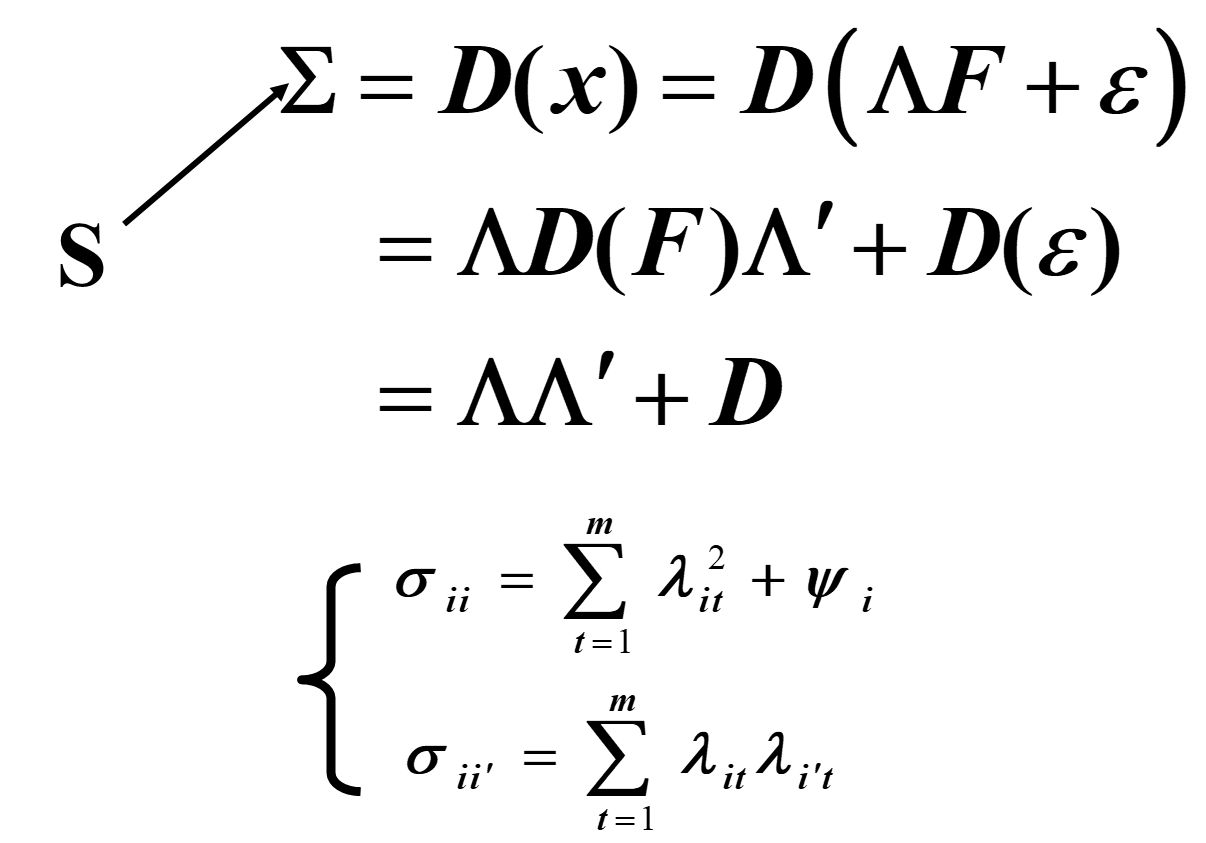
是否标准化?
量纲变换不影响模型,但是影响因子载荷矩阵

标准化后对因子载荷的影响

- 是否对原始变量标准化不影响因子分析的解释,注意要基于因子与原始变量的相关系数解释因子的含义,如果已将原始变量标准化,则可以直接基于因子载荷阵解释因子的含义
- 因子载荷的大小依赖量纲的选取,通常在因子分析前将数据标准化,基于相关阵进行因子分析
因子载荷矩阵不唯一
载荷矩阵不唯一使得因子旋转成为可能

- 好处:不能解释时可以旋转,没有旋转之前认为是没有找到真正有实际意义的因子,旋转帮助我们找到了有实际意义的因子,可以解释实际问题了。
- 坏处:每人得到一组解,谁来确定哪个解是有意义的?增加了人为的因素,不是仅仅由数据决定,这也是统计解决问题的特点。
正交模型中各量的统计意义
因子载荷的统计意义
因子载荷矩阵中每个元素$$\lambda_{ij}$$的意义

变量共同度的统计意义
因子载荷矩阵每行元素平方和的含义,$$x_i$$能被公共因子解释的程度


公因子$$F_i$$的方差贡献的统计意义
因子载荷矩阵每列元素平方和的含义
